Among the few quantum laws that are well-known by the non-scientists, the Tunnel Effect is high-rated, maybe only surpassed by the Schrodinger’s Cat experience and the Wave-Particle duality.

However, few people really understand the phenomenon. In this article, I propose a simple yet effective way to understand the Tunnel Effect with no pre-required scientific knowledge.

What’s the Tunnel Effect?

In this demonstration, I’ll use the simplest interpretation of the Tunnel Effect

A single particle will hurt a potential barrier, which you can think of as a wall. In classic physics, as soon as the particle hit the wall, its speed changes of direction : the particle bounces and starts to return from where it came.

In quantum physics, however, it’s possible (yet usually rare) to find the particle inside the wall or, stranger, after the wall, in the same direction as before, as if the wall simply didn’t exist.

A video explaining the Tunnel Effect

A game-inspired world

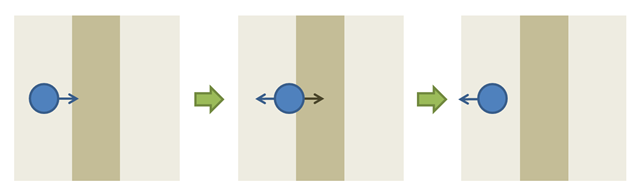
The first and only thing I need to explain the Tunnel Effect is the world as it’s defined in video games. Traditionally, a video game is divided into frames, separated by a small amount of time. Generally, the world occupy 60 different states per second.

Here’s how it works :

1. FRAME n : The objects in the world are in a certain state (position, speed).
   
2. Physics rules (such as gravitation, collisions…) are applied on the objects to alter their speed. Then, based on their speed, the position of every object is calculated as it will be 1/60 second later (this process is known as time integration).
   
3. FRAME n+1 : The objects in the world are in a certain state (position, speed…).

Here’s an image that may help to understand this process :

Handling collisions in time-discrete worlds

In the simplest case, collisions in time-discrete worlds are handled in a very simple way : the particles which collide see the direction of their speed inversed.

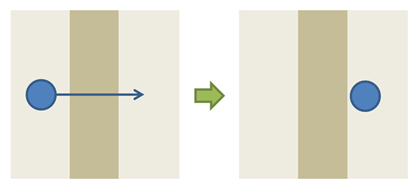
At this time, it’s easy to see how particles can now enter into a wall : they need to enter into a wall before the game engine can detect the collision and inverse their speed :

What is interesting is that, if the ball moves sufficiently fast (or if the wall becomes really thin), it’s possible for the next position of the ball to be located after the wall : the particle didn’t “see” the wall, exactly like in the Tunnel Effect!

As simple as this model may seem, it already helps a lot to understand many Tunnel Effect-based experiences !

Near-realistic model

As interesting as the previous model is, it still features a major difference with the quantum Tunnel Effect : the quantum Tunnel Effect is probabilistic while our model is not. This means that at a sufficiently low speed, our model predict that the ball will never go through the wall.

In the quantum world, this doesn’t happen. Yes, the probability of going through the wall decrease exponentially with the speed (or the wall size) but it never reaches zero. The solution to this problem is really simple, however.

I got the inspiration for the solution from a game I played in my childhood… The game consists of a bunch of player that much go from one side of a place to the opposite one without being noticed in movement by the watcher.

To make that possible, the watcher has to count aloud up to three, at the pace he chooses, while closing his eyes. During this time, the other players have to move as fast as possible. However, as soon as the watcher said ‘3’, he can open the eyes. If a player is still moving at this time, he’s eliminated. Then, the watcher closes his eyes and start to count again.

A video of a large-scale “1-2-3 piano”

What’s interesting is that the time between two “sights” of the watcher can vary a lot! Naturally, most of the time, it will stay around a mean but, to surprise the other players, the watcher can take either a lot of time to tell up to three, or a very short amount of time.

If we transpose this to our game model, we could make the time between two frames probabilistic. While it would stays constant, on average, it would vary a lot during small amount of time.

As such, it’s possible (if the time between the frame just before the particle hit the wall and the next one is long enough) that, even at a small speed, the particle can go through the wall.

Indeed, if the time is long enough, the distance the particle will cover between the frame can be sufficient. However, if the time is as or less long than the usual, it will hit the wall and bounce on it.

Animation showing frames taken at unevenly separated times

Also, even if it’s moving at a very high speed, with a bit of bad luck, a particle can get caught while going through the wall and see its speed inversed.

Another, more physical solution

Another solution to the problem is to factor in a known physical phenomenon known as energy uncertainty.

While, on the long run, the amount of energy in the world stays the same, particles can lean or borrow energy; the amount of borrowed energy conditions how long that energy will stay in the hands of the particle.

That means that the speed of a particle isn’t really well defined. On average, we can measure its speed but, between steps, its speed can vary a lot. Even a “slow” particle can make important progress between two frames if it borrows enough energy.

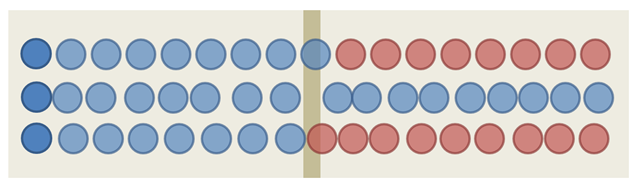
Here’s how the phenomenon looks like (frames taken each ??? nanoseconds) :

As you can see, those three particles progressed at the same pace on average but only one was ‘lucky’ enough to be in a fast phase while nearing the wall. Based on our sample, we can say that a particle moving at that average speed has one chance over three to go through the wall. However, it’s likely that we were very lucky to observe the phenomenon in just three samples. As we would run more samples, we would probably find out a much lower probability.

This explanation is much closer of the physical reality as it uses a real physical phenomenon or, to be more exact, a phenomenon which is part of our current physical models. Meanwhile, I feel that it maybe more difficult to understand: if you didn’t really understand that one, this is not a big deal

Wrapping it up

Normally, if you correctly understood this simple explanation of the Tunnel Effect, you’ve everything you need in hand to understand and correctly solve simple problems based on the Tunnel Effect !

I hope you enjoyed the read,
François