Qu’est-ce qu'un graphe dual?
De manière générale, les représentations de deux problèmes sont dites duales si il existe un lien intrinsèque entre elles de telle manière à ce que chaque instance du premier type possède une instance du second type, calculables facilement à partir de l'autre, et dont les solutions sont elles-aussi liées par ce lien facilement calculable.
Définition de graphe dual
Le cas qui nous intéresse ici est la définition classique du graphe dual. Le graphe dual d’un graphe G est le graphe obtenu en remplaçant chaque cellule d’un graphe par un sommet, et en transformant chaque arrête du graphe G (entre les deux points qu’elle relie) en une arrête du nouveau graphe (entre les deux cellules qu’elle sépare).
Comme on peut le constater sur le dessin interactif précédent, chaque point du graphe original se retrouve désormais au centre d’une cellule du graphe dual ainsi formé. Cela signifie que le graphe initial est le dual de son dual. Cela se vérifie en inversant la construction.
Un exemple connu de graphes duaux
Prenons un ensemble de points. Dans cet ensemble de points, on peut définir deux graphes très importants, qui sont duaux l’un de l’autre par la définition précédente :
Les cellules de Voronoï (ensemble des cellules formées des points les plus proches d’un point de l’ensemble de départ):
Les triangles de Delaunay (ensemble de segments entre les points de l’ensemble de départ définissant une couverture de celui-ci par des triangles dont l'angle le plus petit est maximal, et donc dont les triangles ressemblent le plus possible à des triangles équilatéraux):
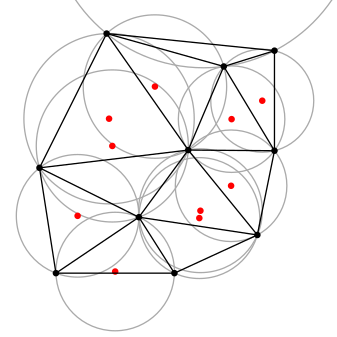
(les points rouges sont les centres des cercles circonscrits aux triangles formés)
Ces deux graphes sont des graphes duaux, car les points de l'un correspondent au (centre des) cellules-triangulaires de l'autre, et les segments sont mappés un-à-un:

(les segments noirs et les segments rouges associés sont perpendiculaires l'un à l'autre mais ne doivent pas nécessairement se croiser; il manque par ailleurs un segment quasi-vertical rouge en haut, hors du dessin lorsque les deux segments concourants se rencontrent)
Cela veut dire que si l’on trouve l’un, on peut aisément trouver l’autre simplement en calculant son graphe dual. Comme ces deux problèmes sont extrêmement intéressants, ils ont tous les deux des algorithmes très efficaces dans certaines situations, et qui ne sont pas toujours les mêmes. Cependant, résoudre un problème dans l’un ou l’autre des graphes est souvent équivalent car il est possible de passer d’une solution à l’autre.
Il vaut donc mieux parfois résoudre un problème dans le graphe dual avec un algorithme efficace et calculer son dual ensuite que de foncer tête baissée et résoudre immédiatement le graphe recherché. C’est un des intérêts des graphes duaux.
Construction des graphes duaux
Il existe plusieurs méthodes pour construire le graphe dual d'un graphe existant. Une des plus efficaces est décrite dans l'article suivant: Graphe planaire et arrangement de droites.